Pitch Perception
Supplement for chapter 23
Sound files:
(soundfile from which the sonogram was made).
From Auditory Demonstrations CD (see discussion here):
-
Circularity in PItch Judgement
-
Stretched and Compressed Scales;
-
Strike Note of a Chime
-
Cancelled Harmonics
-
Linear and Logarithmic Tone Scales (or Logarithmic and Linear Frequency Scales)
-
Pitch of Complex Tones
-
Difference Limenof JND
-
Virtual Pitch
-
Analytic vs. Synthetic Pitch (here, the pitch may seem to go up, or it may seem to go down, depending on whether you are listening analytically or synthetically)
-
Scales with Repetition Pitch (2)
-
Strike note of a chime
-
Pitch paradox
Links
-
Chris Darwin's lectures including discussions of some non-autocorrelation theories of pitch perception:http://www.lifesci.sussex.ac.uk/home/Chris_Darwin/PerMuSo/
-
A contribution based on non-autocorrelatipn ideas by Terhardt and Seewan.
-
Sensitivity to frequency: Just Noticeable Differences of three notes * dead link* - a test of your hearing. Test your sensitivity to frequency differences!
-
PHYSCLIPS Intro to Pitch
Helholtz's Blunder
Yes, Helmholtz. The almost Aristotelian authority on sound. On many auditory topics, his authority has far too much incluence over historic and many modern practioners. His most greivous error, astonishingly central to much of his book, "On the Sensations of Tone", is to blur the distinction between a pure sinusoidal partial, and a "tone", which can be a complex tone like humming, with many partials.or a tone with a definite pitch but missing any partial at that pitch. This sloppiness helped Helmholtz maintain his delusion that "missing fundmentals" or what we now call residue pitch are due to nonlinear vibrations of the ear, causing it to actually vibrate at the frequency of the missing pitch. But, pardon the all caps PITCH IS NOT PARTIAL. A siusoidal vibration, i.e. a partial, produced nonlinearly in the ear or arriving from the outside, would sound just like a partial should sound. Again, pardon the all caps: BUT WHEN WE HEAR A RESIDUE PITCH, WE DO NOT HEAR THE SOUND OF A PARTIAL AT THE FREQUENCY OF THE PITCH, BUT SOMETHING QUITE DIFFERENT: WE HEAR THE SENSATION WE CALL PITCH. Therefore no nonlinear mechanism is needed producing a partial that is not there in the first place: it isn't there if it is missing in the sound arriving at the ear, and the ear does not manufacture it either, for if it did we'd hear the sound of a partial. Pich is a synthetic sensation, an executive summary of sound. Unless only on partial is present in a sound, the sensation of pitch and the sound of a partial are different.
Helmholtz's translator was so frustrated with Helmholtz's sloppiness regarding what should have been the most carfully used word in his book, namely "tone," that he put in a footnote:
"Even Prof. Helmholtz himself has not succeeded in using his word 'Ton' [tone] consistently for a simple tone only..." (i.e. a simple partial) ... (John Ellis, Helmholtz's translator).
Now to illustrate the point, live and in your ears, with this sound file, which first plays a pure partial at the frequency of what will be the missing fundamental or residue pitch of the following complex tone. Listen carefully: the pitch you hear is that of the preceding pure partial, BUT YOU DO NOT HEAR THE SOUND OF THE PURE PARTIAL AT ALL.
Project: Analytic vs. Synthetic hearing
People with training can listen holistically to tones, and they can also parse the same tone analytically, perhaps discerning more than one pitch if present (this is itself a judgement call, however), and going down to the level of hearing individual partials ringing out of a complex tone.
Fortunately no training is required if a simple trick is employed: play the tone, then deliberately oscillate the strength of the group of partials corresponding to a unique pitch, or oscillate an individual partial. It will jump out at you, and even when you restore it to its original strength most people are not able to shut the "analytic" parsing off for a while: you hear the partial or pitch ringing out and you might complain that it has not been restored yet to its original strength!
This is easy to try in Paul Falstad's Fourier. Set up a sawtooth wave in playback, say around 200 Hz, and listen to it. Then grab the e.g. 600 Hz partial "stalk" and raise it in strength. It will stand out. Now lower it back to where it was - you will easily be able to pick it out as an individual partial in the midst of the complex tone. You can most accurately judge when the partial is back to where it began by monitoring the shape of the sawtooth. You are listening analytically!
Residue pitch in a duet
A plausible note from a reed instrument is repeated a fifth above (a factor 3/2 higher in frequency); then the two are combined in a duet. The series f, 2f, 3f, ... of the first, and 3/2 f, 3f, 9/2 f, 6 f, ... of the second note together make of course f, 3/2 f, 2f, 3f, 4f, 9/2 f,.. that formally is a subset of partials based on fundamental of 1/2 f. Of course, some upper partials are missing, and others are shared by both notes, but still the residue pitch is 1/2 f. Do you hear it when the duet is played (klick below)? Last, a note is played down a octave at 1/2 f for comparison.
Also below is Beethoven's "Ode to Joy" played on a synthesizer, but the first five partials of each note are missing. As weird as the timbre is, the tune and pitch is clearly still the same.
From Why You Hear What You Hear....
Prof. Diana Deutsch's Octave Illusion
can be found (along with additional descriptive material) here.
The signal presented to the ears is a continuation of this alternating sequence:
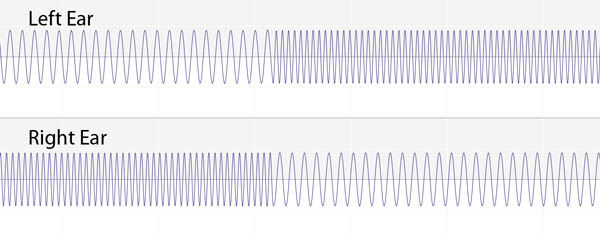
The same site has a number of other illusions, some also discovered by this ingenious scientist.
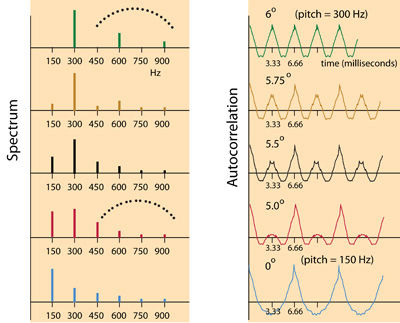
Add higher frequencies - and drop the pitch:
When partials higher in frequency than the initial pitch are added (red, upper right) to the initial tone (blue) in the second half of this sound file (red) , the pitch drops dramatically. The autocorrelation of the signal (lower panels) confirms this drop.

An extended definition of pitch, and a test of Ohm's Law
The end of Chapter 23 makes a case for extending the definition of pitch into the "counting" realm below 20 Hz. We hear a pitch of 5 or 10 Hz quite nicely, thank you! This is different than hearing a partial at say 10 Hz, that we cannot do. The soundfile 10HzMissing.wav has a 10 Hz pitch.
This file is based on a 10 Hz base frequency partial, but has many higher harmonic partials populated, in fact a lump of partials (see the figure below) peaking around 220 Hz. The phases of the partials are all the same, this is necessary to create the sound in distinct pulses. The creation of this sound file and and two variants with one and many phases changed in Falstad Fourier Series is depicted below (a similar case is detailed in the book, chapter 24, using MAX Partials):
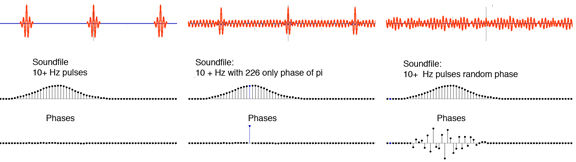
In contradiction with Ohm's Law, changing one phase (middle panel) causes that partial to ring out separately, whilst the main 10 Hz pulsing continues almost unaffected. Thus a phase change has drastically altered what we hear. The last panel, with random phases, is very different again.
The files with one phase changed and with random phases are also provided.
All three sound files have the same autocorrelation function, looking much like the first sound trace, starting at a peak of one of the pulses.
The change in pitch as the holes in a siren are increasingly gathered into pairs, starting with them equally spaced, are understood in terms of the physiological "rules" (as Nature has decided them) connecting pitch with autocorrelation. This can be readily investigated in Charle's MAX Siren, with many variants up to the user.
The Hosanna Bell Freiburg Germany:
http://www.youtube.com/watch?v=KR-4ZMwmBNI * Does no longer exist *
Kettle Drum pitch:
Repetition pitch:
Jean-Francois Charles' MAX Noisy Scale
This patch allows you to select up to four time delayed (with the time delay set by the user via an on-screen piano keyboard) versions of a given white or pink (louder at lower frequencies) noise signal and listen to the results. The time delays are set to discrete values that give the notes of a musical scale as a repetition pitch.

Steam locomotive repetition pitch
Frans A. Bilsen's website has some interesting material based on his own work, "footage" including the sound changes of a steam train passing by, with clear repetition pitch changes, and an animation (with sound) pertaining to this.

Staircase repetition pitch
Article about Chichen Itza staircase repetition pitch, also from Frans A. Bilsen.
Jet airplane repetition pitch
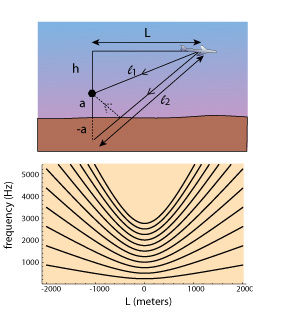
The clear change in pitch as the jet travels overhead, as recorded in a parking lot, is due not to the pilot changing engine rpm, nor is it due to Doppler effects, but rather it is due to repetition pitch changes as the path length of the ground reflection from jet to ear as opposed to the direct path from jet to ear adjusts with position of the airplane overhead.
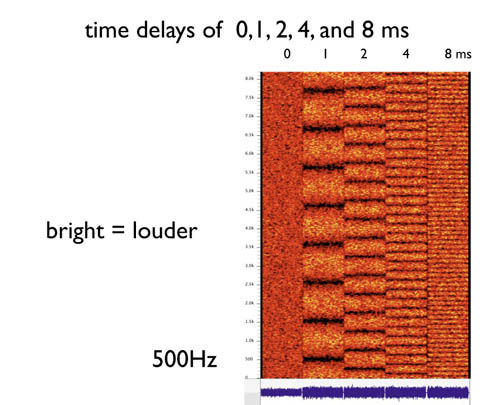
White noise repetition pitch
Although the train and jet are roughly white noise sources, here we provide a calibrated sound file with white noise, and then white noise added to itself with a 1, 2, 4, and 8 ms delay, making 1000, 500, 250, and 125 Hz repetition pitches.
Click tests
Pulses (in groups of 2, then groups of 8) separated by 3, 5, and 7 milliseconds.
Shepard Tones

Shepard tones is a surprising pitch precept. The pitch distinctly rises from one note to the next but after 12 notes it is back where it started! Pitch really does rise every step in this demonstration, going clockwise around the circle in the CDF Applet referenced below.
This pitch perception is logical and correct, it is not an illusion or side effect of other perceptual priorities. Pitch is a qualitative impression like taste, not a quantitative measure of frequency. Once again, the Shepard tones are not an "illusion"! The CDF applet involving Shepard tones featured in this chapter is found at demonstrations.wolfram.com/ShepardTones/.
Shepard Tones from the Wolfram Demonstrations Project by Theodore Gray
(The CDF player is downloadable here)
Jeanne Claude Risset Glissade employs similar trick as does Shepard tones, but in this case to give the impression of a continuously declining pitch, whereas physically, the tone you are hearing is repeating itself every few seconds. Click below:
Risset Rhythm
The same idea that is behind the Shepard and Clisse tones can be applied to rhythms as well. This affirms our extended definition of pitch, stated at the end of chapter 23. We enlarged the idea of pitch to include the frequency of even countable repetitious events much less than 20 Hz, like a 1 Hz tapping sound. A Risset rhythm seems to be constantly quickening, but even after a long time it hasn't picked up in fact! The classic example by Jean-Claude Risset is below.
Project: Chime tone pitch test
Listen to the file and make your choice. To check your decision, analyze autocorrelation of the tone and compare with cosine waves; choose the cosine with the first peak after time zero that coincides with the autocorrelation peak.
Project: Pitch formula for a chime tone (or other tones)
Here we apply the simple formula given in this chapter for the perceived pitch (denoted f, with a bar over it, or f^bar) given a set of partial frequencies f_n and amplitudes a_n :
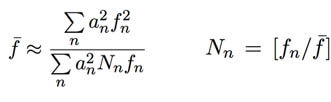
where [...] means "nearest integer to whatever is inside the brackets". This formula is self-referential and a satisfactory set of integers N_n must be found. Usually this isn't too hard, sometimes it is obvious. The example below is meant to help with the idea and the use of the formula. Figure 23.4 in Why You Hear What You Hear shows exactly what is happening.
Basically, N_n is the approximate number of times the n^th periodic sinusoidal (cosine) partial has had a complete 2 pi cycle at the time of the autocorrelation peak at time t^bar = 1/f^bar. Which autocorrelation peak you are looking for is discussed in Why You Hear What You Hear. It may stand out singularly if there is one perceived pitch, or, if there are two or more pitches present, there should be a peak for each of them, differing in the formula by having a different set of N_n.
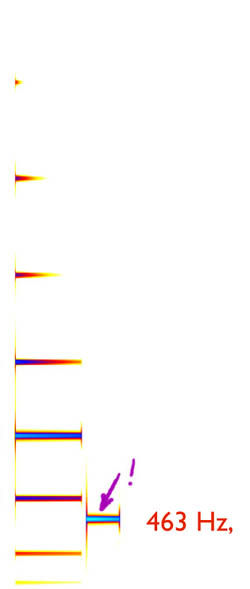
At the left is a sonogram of the chime tone, with a pure partial, 463 Hz, following it, at the pitch most people report when comparing a variable pitch sine tone with the chime. The chime spectrum was analyzed for the amplitude and frequency in each partial, using a spectrum tool in this case in Amadeus, and these were input into the code below (the formula was executed in Mathematica). Note that the perceived pitch is not at any of the partials. The formula, for the N_1, N_2, etc. = 0,1, 2, 3, 4, 5, gives f^bar = 463.6; very close to the perceived pitch. (N_1 = 0 means the lowest frequency hadn't made it back even once at the period 1/f^bar).

Here is the full analysis presented graphically. At the top, we see the chime wave autocorrelation in blue, with a prominent peak presenting itself just after 0.002 seconds. A sine wave at frequency 463 Hz is shown in purple. Since the peaks match, we could could stop here, graphically, and dispense with the formula. Commercial and free pitch finders simply look for the position of the peak numerically, though some go through more machinations with other peaks.
The individual partials are seen oscillating with their respective frequencies and amplitudes in the lower graph. Some are labeled, along with the number of cycles closest to the time of the autocorrelation peak. These go into the formula, i.e. N_2 = 1, etc.
Note that this case is a stretch in that some of the partials do not have peaks falling very close to the autocorrelation peak(the derivation of the formula, not given here, assumes that they are fairly close).
The Mathematica code for finding the peak numerically, and also calculating the pitch formula is shown next; it includes the numerical results.

Music of the Spheres - Literally [from chapter 9]
Suppose we turn the motion of the planets into sound, i.e. try to create the music of the spheres (or the music of at east some of them). Since the orbits are fairly circular (and circular motion, as we know, generates sinusoids. see chapter 3), we will assign a sinusoid a frequency according to a constant times the actual orbital frequency of the planet. To augment the realism, we take the amplitude of each frequency to be proportional to the orbital radius of the planet from the sun.
In the below file, only Mercury, Venus, Earth, Mars, Saturn, and Jupiter are used, the planets known to the ancients.
The frequencies are, respectively, 33 (Jupiter), 84 (Saturn), 528 (Mars), 1004 (Earth), 1613 (Venus), and 4166 (Mercury) Hz. The corresponding relative amplitudes, based on 1 for Earth, are 9.5, 5.2, 1.52, 1, .72, .39. The resulting tone possesses a strong 33 Hz hum tone, with a perceived pitch almost exactly that of Mars, 526 Hz, this raises an extremely interesting point. In chapter 23 we shall learn that pitch need not be one of the partials present, but that perceived pitches do correspond to certain prominent early peaks in the autocorrelation function. These peaks, we shall see, can arise as a combination effect of several prominent partials, but the resultant collective effect is to make a correlation peak at a time that agrees with none of the periods of the individual partials. But what if say 3 partials with periods t1, t2, t3, acting together with given amplitudes, create an autocorrelation peak at time t that coincides with none of these three; this is quite likely. Then a fourth partial with period t4 is added that happens to coincide with t, i.e. t4 = t. Clearly the perceived pitch of period t can only be enhanced. This seems to have happened with Mars: there is a peak in the autocorrelation corresponding to 526 Hz even without Mars included, although not one that causes a pitch dominance. Nonetheless, this peak makes the mars pitch all the more prominent when Mars is added to the mix.
Just Noticeable Difference (JND): Pitch
Here *dead link* is the website mentioned in the book.
Project: Pitch and adding a partial.
According to this idea, if we had an effective pitch f as above (often called a residue or virtual pitch) , and we now add a new partial with pitch f', the impression of a strong, dominating pitch should loom up when f'=f. This scenario is easy to set up in MAX Partials, including variation of the pitch.
Changing the pitch of individual notes in polyphonic music
With many notes playing at once, their partials overlapping, can one go into a recording and change the pitch of an individual note? The Celemony company software does this, and they have excellent instructional videos describing qualitatively how it works. This one is about note pitch shifting.