Dissonance and Temperament
Supplement for chapter 26
Sound files:
"Triad-BarberCompare": Comparing Major triads and barbershop sevenths in Just and Equal temperaments.
"Clarinet4567Equal4567Just" - a version using clairinet timbre.
First chord of A Hard Day's Night, the Beatles (see problem book for questions and discussion).
Very helpful discussion and "Physclips" about temperament and related issues from Joe Wolfe and the University of New South Wales here.
From Auditory Demonstrations CD (see discussion here):
-
Tones and tuning with stretched partials
-
Critical bands by masking
-
Critical bands by loudness comparison
-
Stretched and compressed scales
-
Effect of Tone Envelope on Timbre
-
Effect of Spectrum on Timbre
Stuart Isacoff's wonderful examples of temperament, a companion to his fascinating book Temperament.
List of mean tone intervals
Article on the tritone
Tones and Tuning with Stretched Partials
This is especially interesting and we elaborate on it here. There are four tracks.
One: You hear a four part Bach chorale played with even temperament, using tones having 9 perfectly harmonic partials. Mathematically, the frequencies obey
Two: Both the tones and the inharmonic partials belonging to each tone are stretched by the same amount:

Three: The tones are stretched but not the partials belonging to each tone; this is like an out of tune piano.
Four: The tones are not stretched but the partials belonging to each tone are; *Looks like Two and Four are identical *

From Why You Hear What You Hear....
Chopin piece (section 26.9) in original form and with every frequency downshifted by 208 Hz:
Bell tone: short outtake vs. whole tone. The timbre from a bell struck in the usual manner is quite a bit different from an outtake of the sound file from the same bell, taken some time after the strike.
Grand Piano played forwards and backwards: A remarkable change in timbre accompanies reversing the sound, yet the power spectrum remains unchanged.
Stuart Isacoff's book and sound files
Temperament (Random House) is a wild, nontechnical romp through the controversies surrounding temperament and our eventual "settlement" with even temperament. Isacoff produced some really revealing sound files involving intervals and also excerpts from Bach's Goldberg Variations, found here.
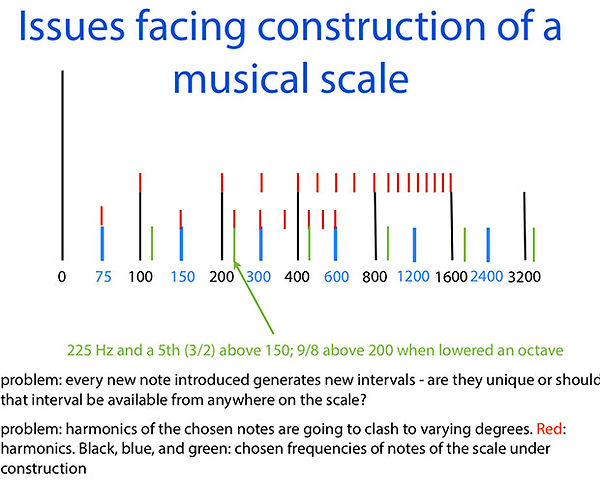
The perfect musical system?
Why You Hear What You Hear makes clear why the heady start to a musical system sketched below, attributed to Pythagoras, becomes a disaster as more notes are added between the octaves. Nonetheless it is instructive to play with a monochord, where two intervals are created for each position of the central bridge; they are each other's inversions in musical terminology.
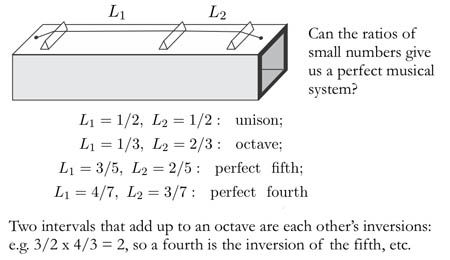
Pythagorean 12 tone Just Intonation
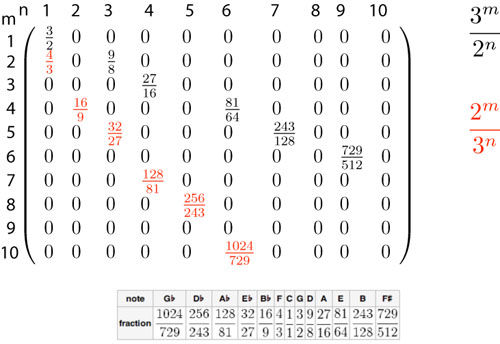
Pythagoras invented a "just" (based on ratios of integers) musical scale based on octaves and the perfect fifth, or 3/2. If inversions are acknowledged, i.e. an interval of a fifth, 3/2, can be followed by another interval to the octave above the first note, that is an interval of 4/3, we see in this way that the scale is built of powers of two divided by powers of three. or their inverses, powers of three divided by powers of two. If you want to stop at a 12 tone system, here are all the possible intervals between 1 and 2, i.e. in the first octave. Some pretty large numbers are involved, that seems to lose the beauty of the perfect fifth, but the beauty is lost anyway because of failure some of the intervals to fall close to consonant intervals, as seen on dissonance maps in this chapter.
Why 12 notes in our Western musical scale?
This site gives an excellent rationale. We reproduce it here, and suggest you visit the site for more information:
"The twelve-tone equal-tempered scale is the only equal-tempered scale that contains all seven of the basic consonant intervals to a good approximation — within one percent — and contains more consonant intervals than dissonant intervals"
Basic Consonant Intervals
-
2/1 octave harmonic inverse of 1/1
-
3/2 perfect fifth harmonic inverse of 4/3
-
4/3 perfect fourth harmonic inverse of 3/2
-
5/3 major sixth harmonic inverse of 6/5
-
5/4 major third harmonic inverse of 8/5
-
6/5 minor third harmonic inverse of 5/3
-
8/5 minor sixth harmonic inverse of 5/4
(Recall an inverse of an interval is the interval that completes an octave. Intervals are ratios, and they multiply, not add. This is in accord with the logarithmic nature of the musical scale. Thus 4/3 times 3/2 = 2, 5/3 times 6/5 = 2. etc.)
-
All equal-tempered scales with 14 notes or fewer, except the twelve-tone equal-tempered scale, contain at most only three of the seven basic intervals (including the octave) within one percent.
-
Several equal-tempered scales with between 15 and 30 notes (notably the 19-tone and 24-tone scales) contain all seven basic intervals, but in none of these scales are the intervals more nearly pure than in the twelve-tone equal-tempered scale.
-
The 31-tone equal-tempered scale has all seven basic intervals to a good approximation, some with better accuracy than the twelve-tone scale, but the most important fifth (3/2) interval is less accurate than in the twelve-tone scale (218/31=1.495).
-
The 41-tone equal-tempered scale is the first with a better fifth (3/2) interval than the twelve-tone scale (224/41=1.5004).
-
The 53-tone equal-tempered scale has all seven basic intervals with a better accuracy than the twelve-tone scale (the fifth is 231/53=1.49994).
The Wikipedia entry on this topic is also excellent and much more detailed.
Organ vs. Trumpet harmony dissonance test raw file:

-
The CDF player is downloadable here
-
Beating of two sinusoids, CDF Player (this can be done more controllably with MAX Partials).
Pythagorean, Meantone, Equal Temperament and other Musical Scales
The CDF applet below is quite amazing. You can hear, sound sample, and visualize standard musical systems, non-standard historical ones, or your own new system, setting the number of notes in the scale and (for your own system) the generating ratio. Hats off to Emmanuel Amiot! The generating ratio for the equal tempered scale is exactly 2^{7/ 12) = 1.49831...
Pythagorean, Meantone, and Equal Temperament Musical Scales from the Wolfram Demonstrations Project by Emmanuel Amiot
Barbershop seventh
A perfectly in tune Barbershop 7th, in the frequency ratio 4:5:6:7, has a residue pitch lower than the pitch of the lowest note being sung. Listen to "4_5_6_7Barbershop" to hear what is going on. Why You Hear What You Hear explains this phenomenon in this chapter.
Java Tuner
Download a simple Java applet to easily explore about ten pre-built musical systems of temperament, including transposition, plus the possibility of adding in your own system. The frequencies of the scales are listed.

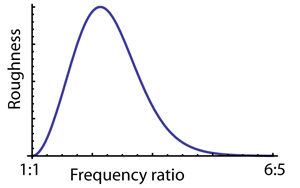
Dissonance Calculator
By assigning penalties for the clash of partials within one critical band on the basilar membrane, two complex tones can be evauated for the degree of dissonance they possess in combination. The more partials that have significant amplitude in the two tones, the more clashes may occur, especiallly if both tones are loaded with partials. Ultimately, the penalty assigned is arbitrary and the results qualitative, but the penalty must at least have the following properties:
-
Zero penalty for partials in perfect unison
-
Rising then falling penalty for partials as a function of difference from unison, in a way which reflects the wider bandwidth of the critical bands at higher frequency
-
Higher penalties for louder partials
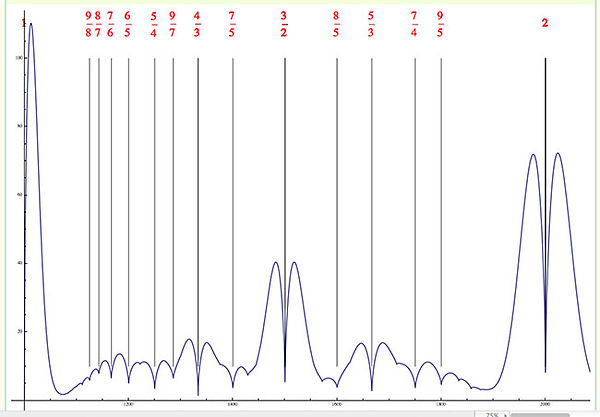
The file here is the Mathematica code; the figure below is the kind of result you get for reasonable penalty function parameters.