Modern Architectural Acoustics
Supplement for chapter 27
Sound files:
From Auditory Demonstrations CD (see discussion here):
70 Effects of echoes
Useful links:
-
Auditory scene analysis: *dead link* Another informative contribution from Oxford University and Jan Schnupp, Eli Nelken, and Andrew King
-
Linkwitz lab; useful formulas, spreadsheet for caluclaiton room modes,
From Why You Hear What You Hear....
An interesting demonstration of very fast echoes in a small office is easy to make. Here we have recorded bubble wrap being popped in an office. That is played back at original speed here. Then, the same sound file is slowed down by a factor of 20. The echoes are now easy to recognize.
String quartet with time delays
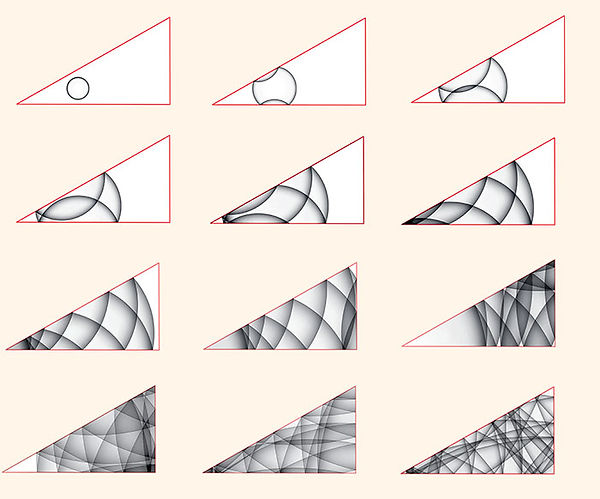
Wedge shaped room with three walls - a triangle
In chapter 12, and in particular in connection with figure 12.2, we considered a localized sound pulse created an "open" 30 degree wedge. A listener standing farther from the apex than the source hears typically 11 echoes plus the direct pusle from the source. (The exception is when the source is in the middle, and there are five double echoes plus a last, eleventh lone echo.) In the figure below, we have a 30 degree right triangle which behaves the same at first, until sound waves hit and reflect from the "back wall" which was absent before, setting up reflections. So, the early history of the closed wedge will be the same as the open one, and the later history will brign an increasing number of reflections per unit time, adding fine structure to the power spectrum seen for the open wedge, figure 12.4, according to the sculpting principle. This means sharper peaks in the power spectrum develop when the echoes from the back wall return, which eventually become very sharp peaks, one for each mode of the triangle, provided there is no dissipation due to losses at the walls. The wave in the triangle roomis shown below, with the "back wall" being the vertical wall at the right:
Measurement of T60
Prof. Daniel Russell of Penn State University has described his measurement and theoretical estimate of the T60 of a small room, including the effect of a carpet.
Acoustical treatments of rooms
Excellent before and after demonstrations *dead link* by a company (Acoustical Solutions, Inc.) that clearly knows how to solve acoustical problems. The following example shows the importance of avoiding repeated echoes from parallel walls (flutter tones); here eliminated by curved reflectors that spread the sound out above and below the perpendicular to the walls:
So, "acoustical treatments" need not be strictly confined to putting up absorbing panels! But, sometimes (often, actually) they are crucial:
Membrane Simulations
Below is the image of the time evolution of a sudden introduction of air at a small spot in a square room, made with Paul Falsatd's Oscillating Membrane. Some browsers (e.g. Firefox on a Mac but not Safari) will work with the sound included version, at http://www.falstad.com/membrane/j2/ *dead link*. For circular drumheads, see here. (Seems to work more universally with sound.)

Pressure is plotted as height; the traveling pulse rises above the flat background, since it represents additional pressure due to the added air. Note that at the four walls, the pressure reflects as a pulse with the same sign, reinforcing itself with double the amplitude within a pulse width of the wall: both incoming and reflected pulses overlap and constructively add.
Room acoustic simulations
The pressure at a source point and wave propagation in a rectangular room is shown below. The red dot show the source point and the recording point for subsequent pressure variations.


Synthetic indoor acoustics
In this chapter we mention the outdoor Jay Pritzker Pavilion, Millennium Park, Chicago, and show a picture. The Wikipedia site has an excellent article showing the arrangement of loudspeakers programmed by a computer to project simulated early and late arriving reverberations of a large concert hall.
The state of architectural acoustics:
Joseph Wechsberg. "Our Far-Flung Correspondents – A Question of Reverberation", The New Yorker, 5 November 1955, p. 90:
"[acoustical consultants] contend … that by applying certain laws of physics and using certain testing devices they can determine in advance how hospitable to sound a new auditorium will be. The fact is, however, that several auditoriums built in Europe recently under the guidance of consultants who presumably applied the laws of physics and used the testing device have turned out to have dreadful acoustics… The sad truth is that while scientists in many fields can foretell with unvarying accuracy what will result from a combination of known factors, those who specialise in acoustics seem to be on no surer footing in making their forecasts than meteorologists are in making theirs. From the evidence, it appears that no one can say for sure what the acoustical qualities of an auditorium will be until it is finished, furnished, heated, and filled with musicians, music, and listeners. And if the qualities turn out to be disappointing, it will very likely be expensive to correct them - if it can be done at all."
We strongly believe this is no longer true, although it was true in 1955, and painfully obvious in the early 1960's as evidence by Lincoln Center, as described in Why You Hear What You Hear. The combination of a better understanding of what parameters people find important, and their optimal ranges, together with robust computer simulations of proposed sound spaces before they are built has made the construction of new halls much less risky than before.
Tokyo Opera City Concert Hall
This relatively new (1997) small concert hall in Tokyo owes a great deal of its success to Leo Branek, the acoustical consultant on the famously problematic Lincoln Center in NYC, and probably the most famous living acoustical consultant in the world. With the advantage of vast experience, computers, intelligence and boldness, Beranek designed a visually and acoustically spectacular space. We highlight it here because of the way it mimics a much larger space, without the use of artificial electronic speakers and time delays, etc. How does it work?

Photo from operacity.jp
The secret is mainly in the ceiling and also the walls: solid oak and intricate, carefully angled grooves that diffract and reflect sound, sending it on a journey of many bounces between surfaces high above the audience (without the power loss from so many bounces being too great, since the surfaces are so hard and non-absorptive). The sound comes raining back on the audience later than one would expect from a modest hall, giving the impression of surfaces much farther away, and room size therefore much louder.
On the lower side and rear walls, much finer and irregular grooving scatters and diffuses high frequencies, reducing "acoustical glare" from smooth shiny surfaces. This is much like the matte surface demo image of a simulation in Ripple, given in chapter 2. See the NYTimes article
Art + Physics = Beautiful Music * subscription required, do you want to link it anayway?*
By JAMES GLANZ, Published: April 18, 2000
This is an informative discussion of the Tokyo City Opera Concert Hall, including its concepts and some of Beranek's history, but it unfortunately does not include the pictures.
Essential video!
An excellent and explanatory video from the makers of Altiverb, an industry leader in impulse response measurement and processing:
http://www.audioease.com/Pages/Altiverb/ *Dead link*
Wallace Clement Sabine's experiments
When Sabine was asked by Harvard's president Charles Eliot in 1895 to improve the terrible acoustics of the Fogg Lecture Hall, part of the recently constructed first Fogg Art Museum (later demolished and replaced). We quote the concise and informative Wikipedia article:
"Sabine's career is the story of the birth of the field of modern architectural acoustics. In 1895, acoustically improving the Fogg Lecture Hall, part of the recently constructed Fogg Art Museum, was considered an impossible task by the senior staff of the physics department at Harvard. The assignment was passed down until it landed on the shoulders of a young physics professor, Sabine. Although considered a popular lecturer by the students, Sabine had never received his Ph.D. and did not have any particular background dealing with sound.
Sabine tackled the problem by trying to determine what made the Fogg Lecture Hall different from other, acoustically acceptable facilities. In particular, the Sanders Theater was considered acoustically excellent. For the next several years, Sabine and a group of assistants spent each night moving materials between the two lecture halls and testing the acoustics. On some nights they would borrow hundreds of seat cushions from the Sanders Theater. Using an organ pipe and a stopwatch, Sabine performed thousands of careful measurements (though inaccurate by present standards) of the time required for different frequencies of sounds to decay to inaudibility in the presence of the different materials. He tested reverberation time with several different types of Oriental rugs inside Fogg Lecture Hall, and with various numbers of people occupying its seats, and found that the body of an average person decreased reverberation time by about as much as six seat cushions. Once the measurements were taken and before morning arrived, everything was quickly replaced in both lecture halls, in order to be ready for classes the next day.
Sabine was able to determine, through the experiments, that a definitive relationship exists between the quality of the acoustics, the size of the chamber, and the amount of absorption surface present. He formally defined the reverberation time, this is still the most important characteristic currently in use for gauging the acoustical quality of a room, as number of seconds required for the intensity of the sound to drop from the starting level, by an amount of 60 dB (decibels)."
The individual Sanders Theater seat cushions became the first standard of acoustical absorption, amounting to "one Sabine" of absorbing power. One Sanders Theater seat cushion is stored, shown here, at the Harvard Collection of Historical Scientific Instruments. *2 dead links*

Project: The foci of an ellipse
Set up Ripple to draw an elliptical wall (set the resolution to 400, uncheck fixed edges). Draw a small circle of wave amplitude near one of the foci. Estimating where an elliptical focus is can be tricky with the eye - they lie closer to the narrow ends than you may expect. Watch the evolution of the pulse you have created - there should be a strong, simultaneous re-formation of a pulse at the other focus, followed by a return to the launching spot, etc. Try other very different launching points.

The Weber brother's 1825 drawing of the result of drops of liquid Mercury at one focus in an elliptical pool of liquid Mercury. The drops were falling regularly in succession - the analog in Ripple would be to have a periodic point source at one focus - try it!

Sabine's spark schlieren experiments in an elliptical chamber, with the spark initiated at the left focus. Notice it converging at the other focus in the lower left.
Isolated resonant mode of a room
In the remarkable pre-computer contour map below, Sabine maps out the sound intensity at head level for a tone input into the famous brick-lined "constant temperature room" where he did many of his experiments. The source was an organ pipe, playing a 248 Hz tone in the center of the room.
It is clear that Sabine has excited a resonant, isolated mode of the room. The room has a kind of quarter-pipe ceiling, and is very reverberant, meaning that 248 Hz is still below the Schreoder frequency (a fact not know to him). Sabine says "To an observer moving about the room it was quite as striking as the diagrams suggest. At the points in the room indicated as high maxima of intensity in the diagram the sound was so loud as to be disagreeable, at other points so low as to be scarcely audible."
